Another approach is to design the implementation around the requirement.
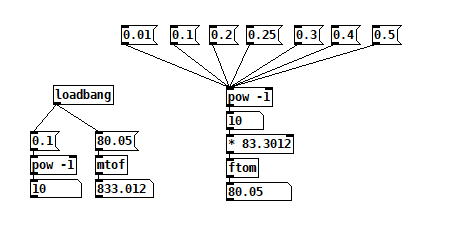
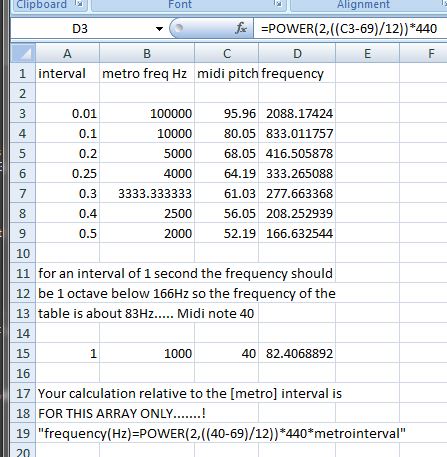
You want to be able to produce a specific frequency. So... make frequency the input parameter, rather than metro time interval.
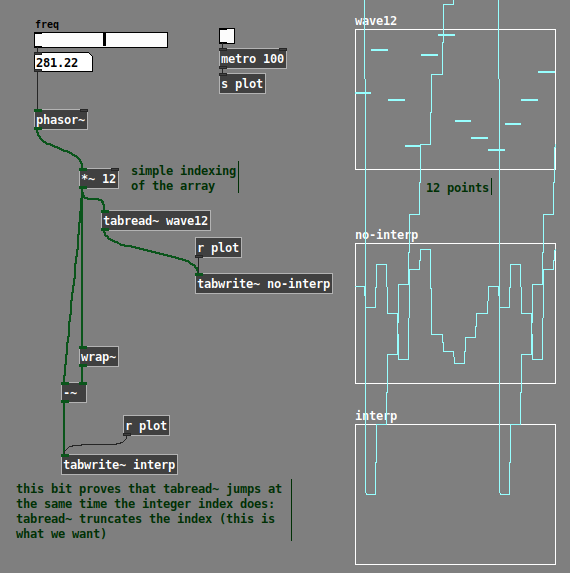
You want to step through array values, with an equal amount of time for each. That suggests a linear ramp, with a given frequency... i.e., phasor~.
phasor~ always goes 0.0 - 1.0. With 12 points, the array indices go 0.0 - 11 -- but here, note that if you say 0.0 - 11.0, then index 0 covers a span of 1, but index 11 covers a span of 0! That doesn't sound right. Instead, define the span for each index as i <= x < (i+1) -- inclusive at the bottom, exclusive at the top. Now the entire range is 0 <= x < 12... leading to the idea of multiplying the phasor by 12 (number of points).
The array indexing should truncate away any fractional part: if (phasor * 12) = 3.546, it should just read 3. Fortunately, this is the normal behavior of tabread~ (not tabread4~).
So we can get a sample-and-hold waveform this way. (The third array is just showing the floor-ed indices, to demonstrate that tabread~ really is truncating rather than rounding.)
All that's left is to add linear interpolation. A standard way to do linear interpolation is:
x = crossfade factor (0.0 - 1.0)
a = value when x = 0
b = value when x = 1
xfade = (b-a) * x + a (this is a reduction of (a * (1-x)) + (b * x)).
If i is the index, then a = array "at" i, and b = array "at" i+1 -- but here, b needs to be modulo-wrapped back around, because i+1 could be 12-point-something. Pd vanilla doesn't have [%~] at signal rate, but [expr~] has fmod().
So we can index the two values, subtract, multiply by the crossfade factor (which is phasor * 12 --> wrap~), then add the "array[i]" value back in.
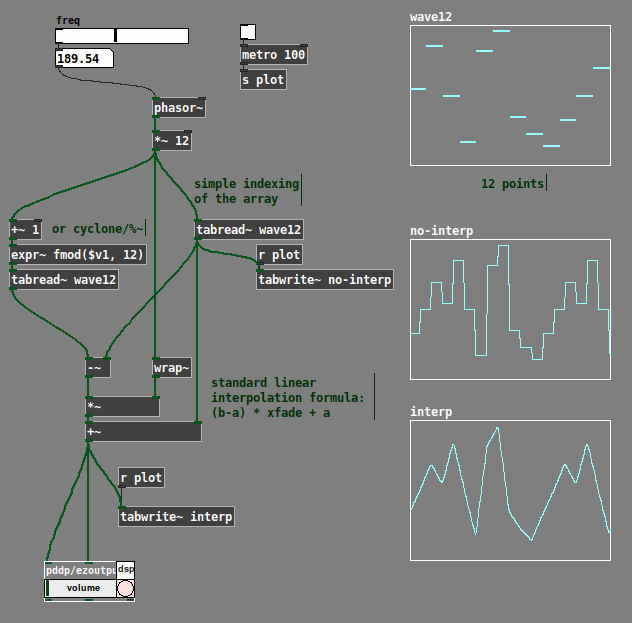
23-0408-linear-gendy-2.pd
Now you can do whatever frequency you want, without the awkward conversion. Doesn't matter what that online tutorial said, IMO this fits the stated requirement better.
hjh






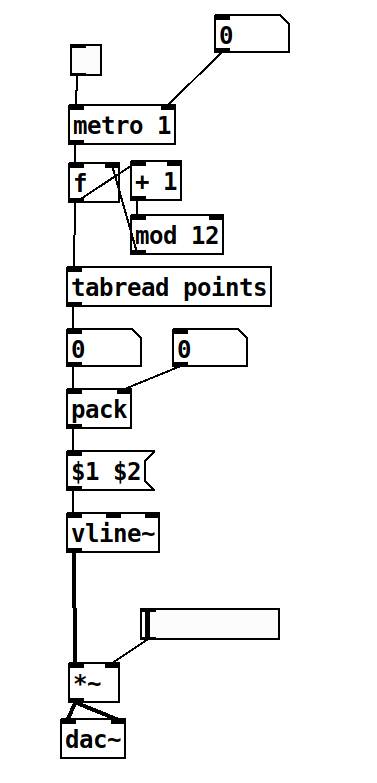

 (though I have to admit it wouldn't handle the random segment time gracefully -- you could modulate the phasor~ frequency but the ramps between points would not be straight lines -- I thought about how to do that but it seems tricky).
(though I have to admit it wouldn't handle the random segment time gracefully -- you could modulate the phasor~ frequency but the ramps between points would not be straight lines -- I thought about how to do that but it seems tricky).
