Hi,
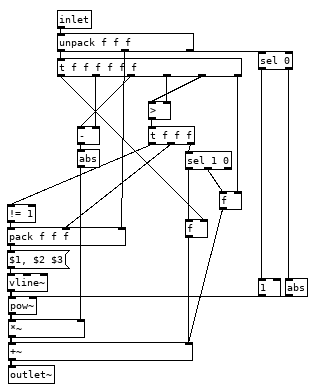
I need to be able to convert a value within a given range to an exponential value within the same range. I made an abstraction "autoscale" which remap the highest and lowest received values to a given range.
If incoming is 0.3 and the lowest value so far been 0.2, the highest so far has been 1.2, and the range is set to 3 and 7 the output will be 4.
I would like to be able modify the output value to an exponential or logarithmic curve where you can set the curve steepness.
What options would there be to solve this? Could I have a function within an expression object? Or use an array? Please show me.
Once I got that going I need to be able to set the curve so that a given value will end up as the exact half of the scaled range. Using the values in the example above incoming value 0.3 should then output 5 after the exponential curve has been set.

Cheers!