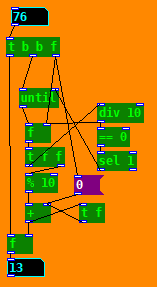
I am sitting with a little patch here... I want to calculate the digit sum of an integer.
What I have so far works with any integer up to and including 99. But the trouble starts at n >= 100.
See the patch attached: DigitSum.pd
I got this working in Python, for any integers:
def digSum(n):
out = 0
while (n != 0):
out = out + int(n % 10)
n = int(n/10)
return out
for x in range(1,200):
n = x
print(n, ":", digSum(n))
But [expr] seems to not do while-loops, unless I am mistaken?
I have tried sloppy workarounds, chaining up multiple [expr} objects, but it's error-prone, ugly, and convoluted.
The end goal is to be able store the digit sums of a given range of integers in an array; Like you can see in the right-hand section of the DigitSum.pd patch.
Anything I am missing here?