See pictures
Shouldn't the first harmonic of cosine just be a 90 degrees out of phase sine instead of a constant ?
Message fro both sinesum and cosinesum
-
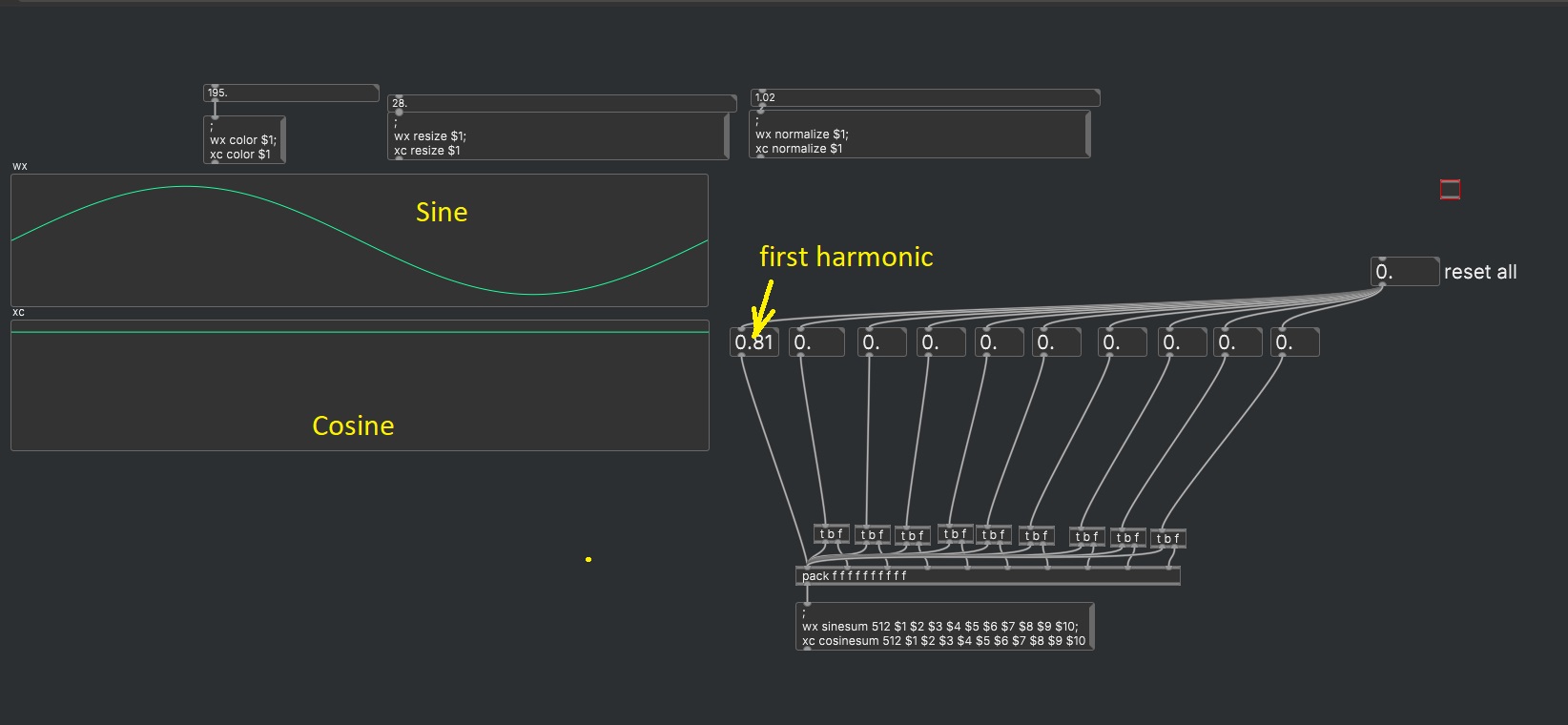
Why is the first harmonic of the cosinesum a constant dc ?
-
cosine and sinesum correspond to the 'real' and 'imaginary' parts of the 'real' fourier series respectively. since there is no imaginary part for frequency 0 (dc) I guess it's skipped for sinesum. see the help file of
[rfft~]for some more info. (beyond that you'd have to start learning about dsp) -
You will also notice that if N is the power-of-2 table size, the (N/2th) coefficient of sinesum is mostly noise, whereas the ((N/2)+1)th coefficient of cosinesum is Nyquist.
-
@seb-harmonik.ar said:
cosine and sinesum correspond to the 'real' and 'imaginary' parts of the 'real' fourier series respectively. since there is no imaginary part for frequency 0 (dc) I guess it's skipped for sinesum. see the help file of
[rfft~]for some more info. (beyond that you'd have to start learning about dsp)It's only skipped for cosinesum (lower table ) and not the sinesum (upper table) , the screesnhot shows the first partal for sinesum and a DC constant for cosinesum
( sinesum and cosinesum and their $1 $2 etc partials are combined in the same message ) -
@gentleclockdivider said:
It's only skipped for cosinesum (lower table ) and not the sinesum (upper table) , the screesnhot shows the first partal for sinesum and a DC constant for cosinesum
This means that the cosinesum preserves the zero-frequency component, while sinesum skips the zero-frequency component.
sin(0x) == 0, so there is no need to keep it.
cos(0x) == 1, so if it's skipped, then it becomes impossible to synthesize a wavetable that has a DC offset.
That's probably the reason for the different behavior. It's a bit surprising but not unreasonable.
hjh

