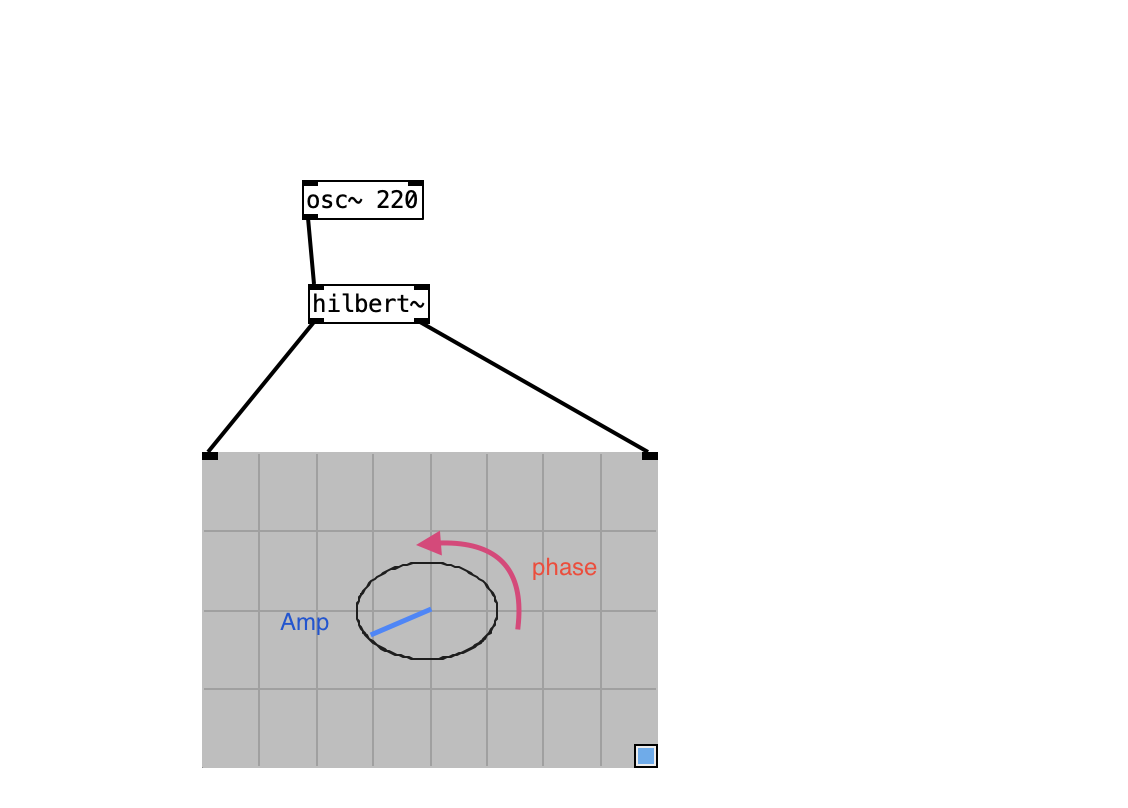
[phasor~]
|
[cos~]
should be the same as
[osc~]
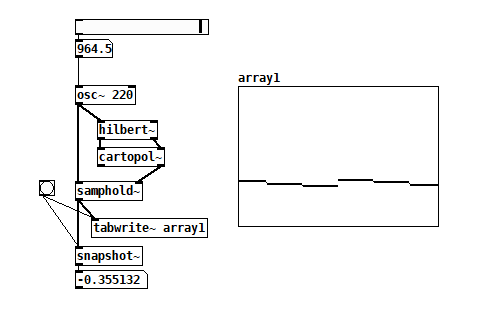
but this time I need to measure the phase of [osc~]
and do the same as
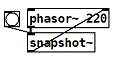
with [osc~] instead of [phasor~].
I have a running patch, but sometimes it flips the phase by 180 degrees.
Do you know why or how to avoid that?
Here is the patch:
phase_of_normalized_cosine~.pd
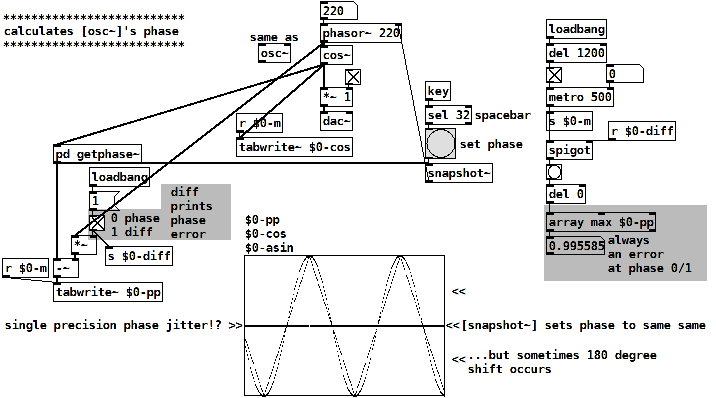
The patch calculates the phase of a normalized cosine y(x) by
asin(y(x)) / (pi/2)
this is a triangle wave, following cosine's shape linearized.
Then a tri-to-saw waveshper:
invert the falling part of the triangle
and divide it's frequency by 2.
late EDIT: also read this: https://forum.pdpatchrepo.info/topic/15128/snapshotting-and-restoring-the-state-of-a-phasor-exactly