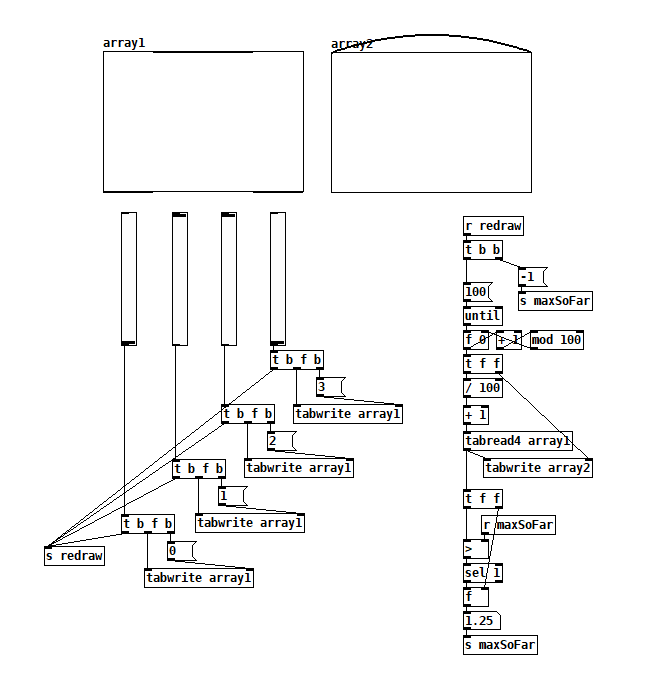
This is really a math problem, but I noticed that with some volume-maximized pop music, using 4 point polynomial interpolation to implement varispeed can increase the peaks and cause clipping.
Here's a control rate demonstration: overshoot.pd

Is there a theoretical or practical limit to this kind of peak increase?

@jameslo I think what you have is "ringing" because of the very sharp changes. Your test must be the worse case scenario......... https://en.wikipedia.org/wiki/Ringing_artifacts
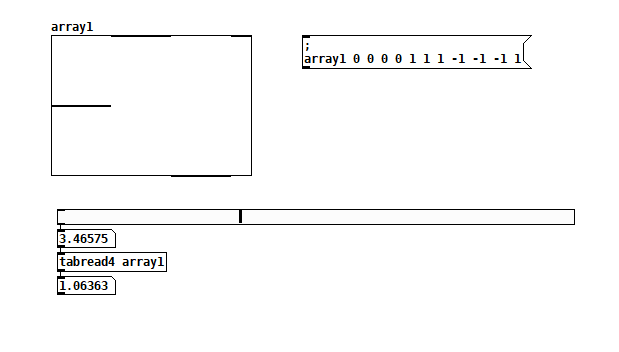
You can see it if you plot the output.

For a sine wave there should be no overshoot and for a complex signal not as much as you have in your test.
A [/~ 1.13] should fix it if I am right.
David.

@whale-av I'm not sure that ringing is relevant or helps quantify the issue, but I support all efforts to keep Spinal Tap relevant in international discourse.

I found this explanation of 4 point interpolation helpful: interpolation.pdf .
It's kind of surprising how straightforward it is to construct a 3rd degree polynomial that hits all 4 points, and useful to know that the resulting polynomial is only for interpolating the interval x2..x3. That explains why tabread4-help says "Indices should range from 1 to (size-2) so that the 4-point interpolation is meaningful", e.g. if you have a 4 point table, you can only interpolate between indices 1 and 2 (the 2nd and 3rd table value). That in turn implies that I only need to characterize the overshoot produced by any given vector of 4 consecutive samples because everything before and after doesn't matter. You can see it in @whale-av's plot--those sharp points at some of the integer indices as the algorithm switches abruptly from one polynomial to another.

In a cursory search of the web I can find tutorials on how to find the local minima and maxima of a given 3rd degree polynomial, but not a family of them (varying over all yn). I think this means I need multivariable calculus to answer my question analytically. Which in turn means it's probably not happening.

@jameslo You are not normally known for giving up....!!
However, I am unsurprised...... it is a problem for medical, geological, climate, space travel and other engineers...... and even mathematicians........ https://math.stackexchange.com/questions/450328/what-is-the-maximum-overshoot-of-interpolating-splines-in-d-dimensions (no solution in nearly 9 years).

And then I remembered that Pd is much better at solving such problems than any of those "scientists" .......
(for our very limited use)
David.
Glory to Splinal Tap

It smells like 1.25 is the limit: graph overshoot.pd