Playback rate Phasor~ II.pd
2021-10-22_23-42-55.mp4
Hi,sorry for my bad Enlish.I'm designing a sample player that can play faster or slower then normal speed, play forward and reverse.It is mockup of VCV's NYSTHI-MUSICALBOX plugin. I mainly use |phasor~| and |tabread4~| to calculate the frequency of |phaosr~| by setting the start and end points, and the signal given by |phasor~ is mapped into an index and given to |tabread4~|.
The problem is: when changing the start and end points there will be an obvious audio click, the starting point can be used |samphold~| to do the logic to take effect the next time you play, but the audio click that occurs when changing the end point really do not know how to do.

Translated with www.DeepL.com/Translator (free version)

@Jamin-hou I am not an expert in Pd Audio. I use a "duck" like the DJ or radio presenter who wants the music to fade down as he speaks.
The problem with changing the play points is that the sudden changes of sample levels are perceived as clicks.
Here......... https://forum.pdpatchrepo.info/topic/13641/best-way-to-avoid-clicks-tabread4/12 I gave an example of how to "duck"..... fade down to zero and back automatically as points are changed.
You can reduce the fade times to about 3 or 5 milliseconds and not hear the change.
David.

@Jamin-hou You need to samplehold~ the value of start and end so that it doesn't change while the phasor is going from 0 to 1, otherwise there will be jumps in its progress (and hence clicks).

Even with this change, you will notice that the pitch is not steady as you adjust the start and end. If you want that to go away, you also have to samplehold~ the start and end values used in your expression. You also have to adjust for negative frequencies so that the samplehold~ samples on the jump from 0 to 1.

@whale-av said:

I am not an expert in Pd Audio

Whatever you say, boss

Hi Junzhe

I often like to think through something like this with a concrete example.

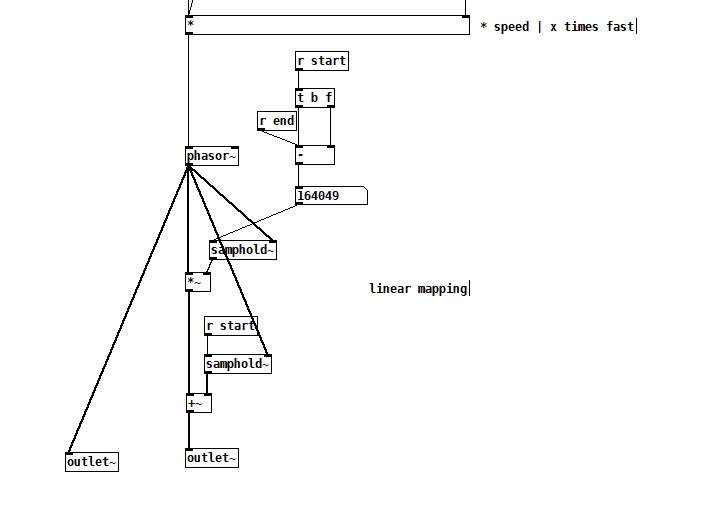
Let's start with 10 seconds of audio: phasor = 0 --> time 0, phasor = 1 --> time 10000 (ms).

Then, at 5000 ms, you change the end time to 7000 ms.

So, now, phasor = 0.5, time = 5000. And you need phasor = 1 now to map onto 7000 ms.

So two things need to happen:

1. The phasor, running at its current speed, would reach its end 5000 ms later -- but you actually need it to reach the end in 2000 ms. So the phasor's speed has to increase by a factor of 5/2 = current_time_to_end / new_time_to_end.
2. The linear mapping currently locates phasor = 1 at time = 10000, but now you need phasor = 1 --> time 7000. So the slope of the linear mapping will have to adjust by a factor of 2/5 = new_time_to_end / current_time_to_end (and the linear function's intercept would have to change too).

The changes in phasor frequency and linear slope should cancel out.

Then, at the start of the next cycle (which can be detected by [samphold~]), you would have to recalculate the slope for the entire start <--> end segment.

I might be overthinking it, but e.g. jameslo admits that in a simpler solution "the pitch is not steady as you adjust the start and end" so I think there aren't many shortcuts to be taken.

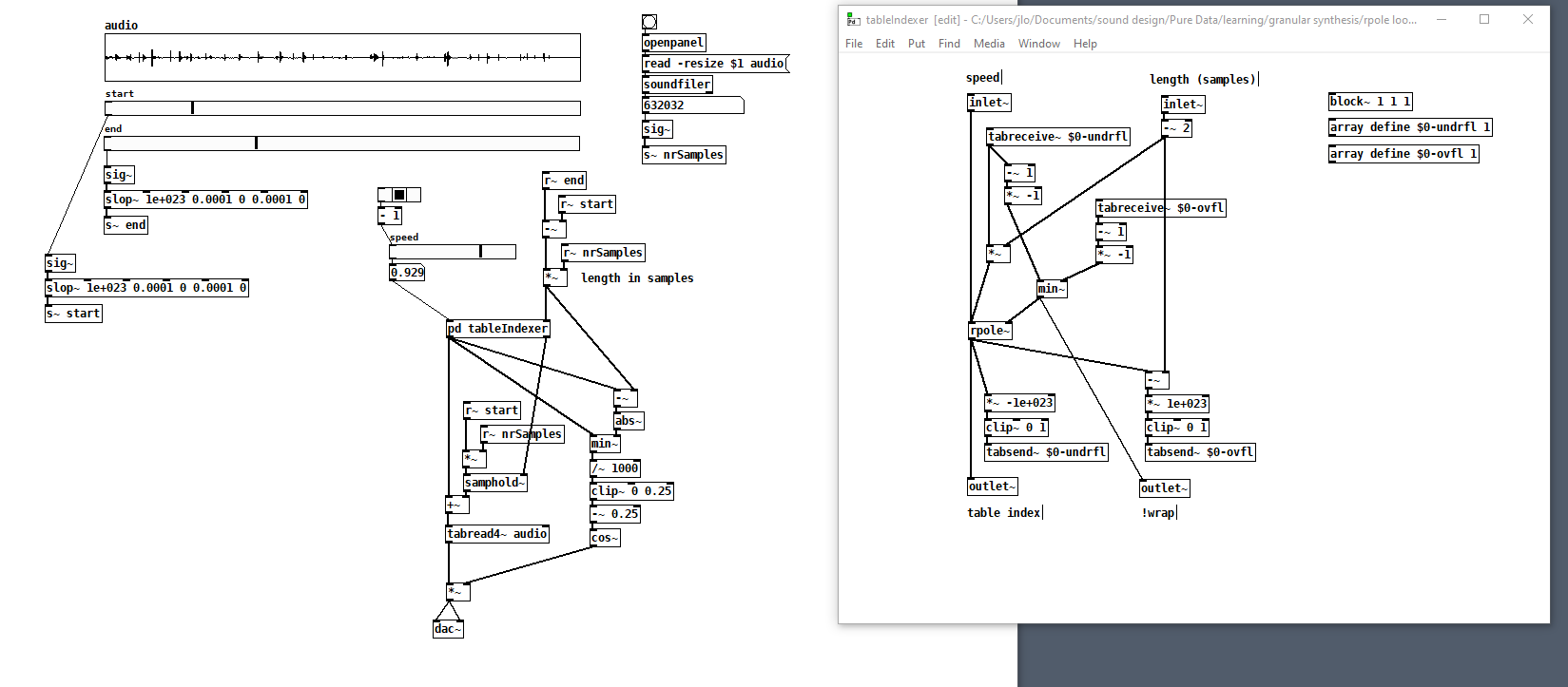
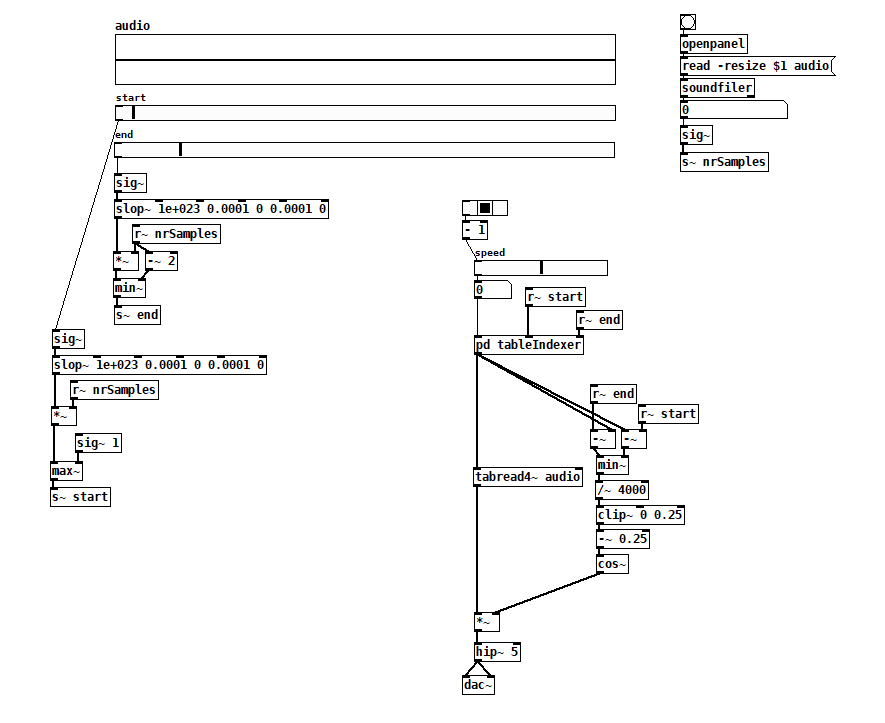
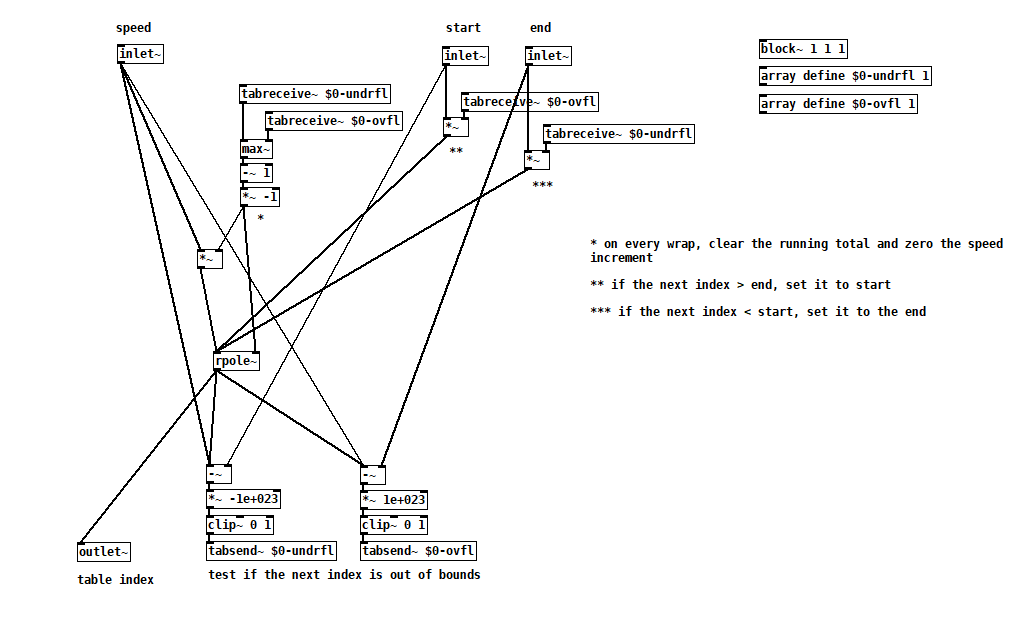
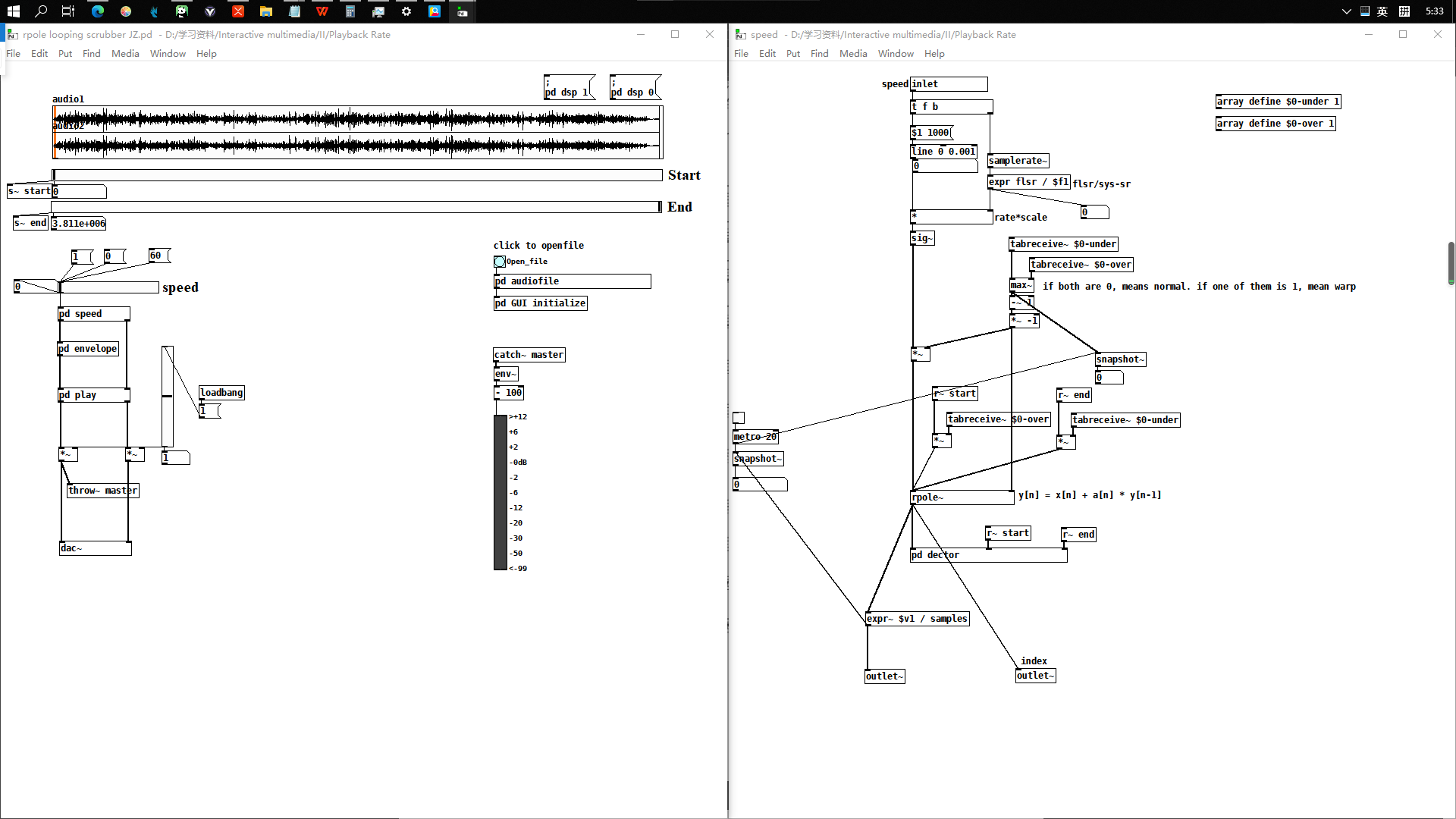
BTW there is another way to integrate a rate: rpole~. With an integrator, you don't have to worry about rejiggering slopes -- it just continues on its way, and reaches the end value in its own time. But, you would be responsible for triggering the reset at that point. This version uses control messages for triggering, so it would be quantized to block boundaries. To do it sample-accurately involves feedback and I never worked that out.

integrator~.pd :

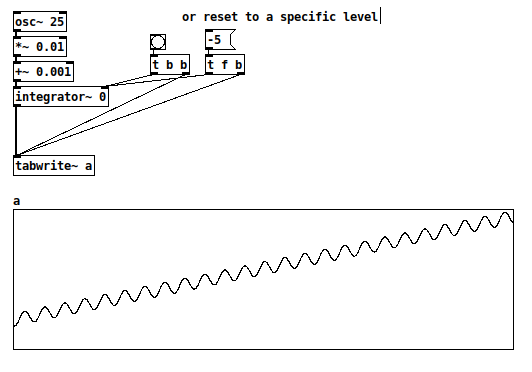
And a quick test patch (array "a" is 44100 samples, vertical range -10 to +50):

hjh

PS Hm, now I guess the [route float bang] isn't needed after all.

@ddw_music I guess if you wanted to use rpole~ for table indexing to make speed changes immediate and continuous, you might call it a looping scrubber? rpole looping scrubber.pd

@jameslo WOW~amazing！太棒了！Ilike it！this is exactly what I want to create!
I found a little problem ：if sample rate（in audio setting） changed the result sound different in your patch.
and I don't quite understand this part：
|*~ -1e+023|
|
|
|clip~ 0 1|
why times that huge number and then clip？
Would you mind explaining that part?I am really confused;-)

Junzhe hou

@ddw_music Hi professor!?!? good to see you here! I read your email last week but im so confused with your
patch--varispeed-segment:

|noise~|
|
|lop~ 3|
|
|*~ 30|
|
|+~ 1| |value f1scale|
\ /
|rople~|

You method "L inlet = rate * scale for sample increment",so is the rate always changing?

wow You helped me in class and now you helped me after class. I can't thank you enough，really！！！

Junzhe

@Junzhe-hou I'm not sure why that patch wouldn't work at different sample rates. Are you sure the file you are loading and your audio interface are compatible with that different sample rate?

That combination of objects computes the same thing as [expr~ $v1 < 0], i.e. output 1 when the signal is negative, 0 otherwise. That plus the thing to the right is just to detect when [rpole~] underflows or overflows, respectively. It would've probably been clearer just to use [expr~].

@ddw_music I'm sorry if I just did your student's homework

Edit: Hmm, I'm not sure why I didn't treat the start index the same way as I treated the end index. That's probably the next thing to try. so that the samplehold~ on the start index isn't necessary. I also think there might be improvements to the wrap around indexes given the recommendations on using tabread4~.

@Junzhe-hou said:

@ddw_music Hi professor!?!? good to see you here!

Yes, it's me -- I almost didn't notice your username

I read your email last week but im so confused with your
patch--varispeed-segment:

|noise~|
|
|lop~ 3|
|
|*~ 30|
|
|+~ 1|

This is just a way to generate a modulator for the playback rate. It could be any other modulator (LFO, envelope, anything).

After that, this is multiplied by a sample rate scaling factor.

As you asked jameslo: "if sample rate (in audio setting) changed the result sound different":

• If the file sample rate is 96 kHz and the soundcard sample rate is 96 kHz, then normal-speed playback is to move forward exactly 1 sample in the file for every output sample.

• If the file sample rate is 96 kHz and the soundcard sample rate is 48 KHz, then normal-speed playback is to move forward exactly 2 samples in the file for every output sample. (If you playback at 1:1, then the file will sound slower at the lower soundcard sample rate.)

This was one of the big reasons for me to make [soundfiler2] in my abstraction set. It calculates file_sr / system_sr and saves this in a value object named after the ID+"scale". If you multiply the playback rate by this scaling factor, then the file should sound correct at any system sample rate.

(BTW you would have the same issue in SuperCollider: PlayBuf.ar(1, bufnum, rate: 1) will sound different depending on the hardware sample rate, but PlayBuf.ar(1, bufnum, rate: BufRateScale.kr(bufnum)) would sound the same, except maybe for aliasing when downsampling.)

You method "L inlet = rate * scale for sample increment",so is the rate always changing?

Yes -- variable-speed playback.

@jameslo "I'm sorry if I just did your student's homework" -- actually this isn't for my class -- independent project. There are still some students who do hard things just because it's fun to overcome challenges

hjh

Here's a less sloppy version of that same rpole scrubber. It treats the loop endpoints symmetrically, wraps to and from the actual endpoints (and not one index off), and limits the endpoints to valid indexes for 4 point interpolation.
rpole looping scrubber.pd

tableIndexer:

Edit: ugh, I see now that the slew rate limiters on the start and end sliders aren't doing what I thought they were doing. What should happen if, when it's playing forward, the start point is moved such that it passes the current play point? (and vice versa for backwards play and the end point moving forward)

@jameslo Thank you soooooo much jameslo!Your patch inspire me a lot!Although it takes me about 2 hours to understand it
I made another version base on your |tableIndexer| idea. And I add |file sample rate/system sample rate| to prevent pitch shift.Well......two things I still don't understand:

• I used |expr $v1<start| in my patch directly but I got message ：receive~ end: vector size mismatch,receive~ start: vector size mismatch.After I deleted |block~ 1 1 1| there was no such message,I'm not sure if they're relevant.

• I notice you use |nrSamples - 2| to valid indexes for 4 point interpolation.But when we apply sinesum function like:|;array1 sinesum 128 1 1|,then there will be 131 samples in array1. So should we add point into it like tabosc4~ help.pd says:'one at the beginning and two at the end, which should be wraparound copies of the last point and the first two points, respectively', but Im confused by tabread4~ help.pd....it did say 'Indices should range from 1 to (size-2)'
  rpole looping scrubber JZ.pd
  rpole looping scrubber JZ.mp4

Looking forward to the reply,have a nice day!

@Junzhe-hou RE {expr~ $v1 < start], that's not really the issue because you didn't literally write that (I just tested if expr~ can contain the names of audio signal receives, and Pd told me "no"). The issue is that you are trying to send a signal from an enclosing patch with the default block size (64 samples) to a subpatch with the minimum block size (1 sample, i.e. [block 1 1 1]) and s~/r~ won't reblock the audio vector for you. I think only [inlet~] and [outlet~] do that, that's why my example works.

The reason I'm using the minimum block size is so that I can feedback audio data with the minimum latency possible. In this case, I'm testing whether the next index is beyond the range start..end and using the output to turn on and off different inputs to [rpole~]. Can someone suggest a good example in the Pd help system?

RE sinesum, yes, it increases the table size to pad the table to the size needed for [tabread4~], but in my case I'm loading a sound file so I'm just throwing out the first and last sample to stay within the legal [tabread4~] boundaries. An N sample soundfile is addressed with indexes 0..N-1, so to pad the ends, the lookup indexes have to go from 1..N-2. I hope this makes sense. @ddw_music could probably explain it better because that's what he does!

@jameslo said:

@ddw_music could probably explain it better because that's what he does!

Actually I'm not controlling for that in these abstractions, pretty much leaving it up to the user. (I think... I haven't learned enough yet about making readable patches, so I might be misremembering what I did.)

hjh