I expected this patch to display a constant 0 or maybe a constant 1, but it displays cyclical noise just above 0. Why?
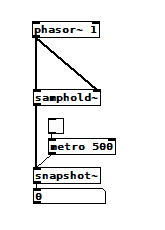samphold~ noise.pd

@ddw_music Maybe, but it is the same calculation every time so why would the errors accumulate?
No problem with [line~] or [vline~] into [samphold~]
[phasor~] phase not updated except at block boundary? I tried a single sample block and there was no difference........
Changing the Pd samplerate does compress the pattern. At 200K sample rate the deviation is considerably reduced.
FFT...... I agree..... still probably phase.
Does anyone have [vphasor~] compiled?
https://forum.pdpatchrepo.info/topic/10192/vphasor-and-vphasor2-subsample-accurate-phasors
David.

@whale-av I think @ddw_music is saying that each point in the phasor except for the jump downward is generated by adding an incremental amount to a running subtotal. That amount is a function of the frequency, and if its calculation contains round-off error, then that error accumulates in the subtotal. It's consistent with that nice graph you showed, assuming that the jump downward is produced by something that doesn't zero out the accumulated error.

I think this patch shows that [phasor~ 1] drops a sample every 5 seconds or so, i.e. it runs a little fast:

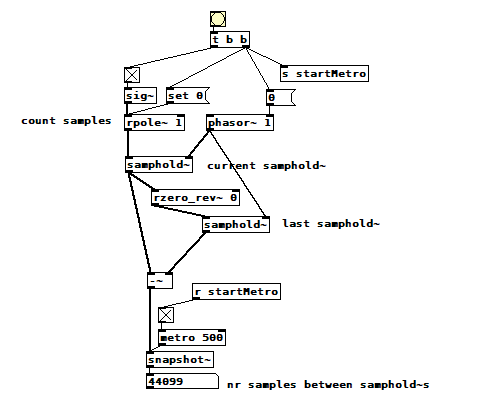
phasor~ timing.pd
I suppose I could/should get off my lazy rear, learn something about github, download the source, and search through it, but I'd rather continue slogging through katya's blog.

@jameslo the phasor~ source was a bit confusing to me at first, it works by setting the upper 32 bits of a double (including the exponent) such that bit 32 of the double represents the "1s" place value, so all of the lower 32 bits represent the fractional part. Then after the correct phase accumulation is added, the magnitude that was added to make all lower 32 bits the fractional part is subtracted from the double in order to output just the fractional part. (and then the upper 32 bits are again set to that value, destroying the non-fractional part)
All of this is done to avoid cpu branching so it can pipeline instructions better (so instead of having to check if the phase > 1, each sample you just set bits to a certain value)

@jameslo just investigating further: the closest that a 32 float value can come to representing 1/44100 seems to be 0.00002267573654535226523876190185546875. However, since bit value 32 must be 1 and because the exponent of this number is 2^-16, that means that once this number is added to 1572864 as a double the fractional part can only represent
0.0000226758420467376708984375

0.0000226758420467376708984375×44100 = 0.00000463426113128662109375
as the fractional part of the first "wrapped-around" sample (I might be missing something, but something like that is probably happening)
edit: actually after testing this matches exactly with the behavior of your first patch (1st wrap-around is that # after sending "1" to the phase of phasor~ and the toggle at the same time)

@seb-harmonik.ar (full disclosure: I'm barely hanging on...) OK, is it consistent with my last patch, the one where the phasor falls short one sample every 5 seconds? I didn't say it, but that seemed like way more than accumulated single-precision floating point round-off error to me, which is why I'm insecure about my conclusion.

Just to clarify, are you saying that the accumulator is single or double precision floating point? Maybe even simpler and more to the point, are you confirming @ddw_music's round-off error accumulation theory?

@jameslo yes, @ddw_music was correct. It's a combination of double and single precision (and I edited my last comment, this prediction is consistent w/ the 1st patch at least). The value "conv" in the source code is stored in a t_float, which is generally a 32-bit float these days (though maybe that will change soon..). This is set to 1/samplerate. every sample conv is multiplied by the input frequency (which is also a 32-bit float) and then added as a double to the current phase, which is a double with value 1572864 + actual phase, (1572864 is 3^19, a float value that makes bit 32 of the entire 64-bit double value the 1s place, leaving the remaining 32 bits as the fractional part). Every sample the top 32 bits of the phase are set to the top 32 bits of 1572864, and when the phase is output, 1572864 is subtracted from it.

tldr: the phase accumulator is basically 32-bit fixed-point

@jameslo Just for information.
If the sample rate is a power of 2...... 32768Hz for example...... there is no drift.
I wonder whether your RMS an FFT results would converge at such a sample rate?
David.

@whale-av that makes sense bc powers of 2 are easily represented exactly in binary floating point (so the increment can be represented exactly without roundoff error)

@whale-av said:

I wonder whether your RMS an FFT results would converge at such a sample rate?

He he he, they don't. I'm glad because if they did my head would explode.

@seb-harmonik.ar said:

the closest that a 32 float value can come to representing 1/44100 seems to be 0.00002267573654535226523876190185546875. However, since bit value 32 must be 1 and because the exponent of this number is 2^-16, that means that once this number is added to 1572864 as a double the fractional part can only represent
0.0000226758420467376708984375

Wait, that is consistent with my second patch--the increment is slightly large, and so the phasor reaches its peak a bit early, i.e. its running a bit fast. In numbers, the increment is ~ 0.106e-9 too big. That times 44100 times 5 is greater than 23e-6, which is greater than 1/44100 as a 32 float, i.e. 1 sample.