In the help patch for [biquad~] there are coefficients for a very narrow bandstop filter centered at 5512.5 hz @ 44.1k or 6000 hz @ 48k. The filter's Q isn't stated so I thought I could reverse engineer it using those coefficients as my key but I can't seem to generate them exactly by using either my own coefficient calculator or the one from ELSE (bicoef2). I get close with a Q of about 3500, but I can't match all coefficients with a single Q value (I can't remember if the 1s are even posssible). Why would that be?
help coefficients search.pd

@jameslo Being incapable of all understanding of the cookbook I have always used [notch] [lowpass] [equalizer] etc. from the ggee library..... there are quite a few of them.
Bandwidth in octaves (value 100 = 1 octave) but 1 am not sure that is linear for calculating Q.
Of course you can print the coordinates produced by the objects.
Maybe they will help your research though..?
David.

@whale-av I thought I had figured out the relationship between Q and BW but my patch failed miserably. So I just went with BW but got the same "close but no cigar" results:

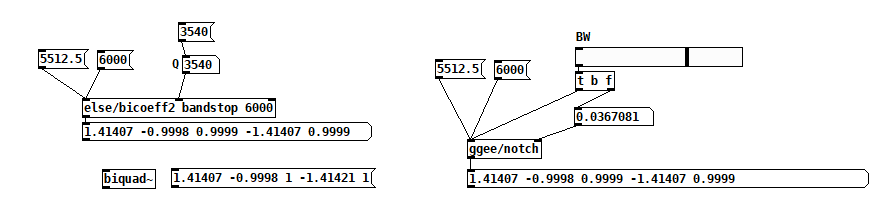
Edit: looking back at that cookbook formula for notch coefficients (https://webaudio.github.io/Audio-EQ-Cookbook/audio-eq-cookbook.html), ff1 and ff3 are defined as 1/1+alpha, so the only way that could equal 1 is if alpha equals 0. But alpha is defined as sin(2 * pi * f / sr) / 2 * Q, so f would have to be 0 or Nyquist, or else Q is so large that it underflows the precision of the floats used to calculate the coefficients? And if it's the latter, then that seems like a weird thing to present as an illustrative example. (Note that in the example, f = 5512.5 = Nyquist/4--prob not a coincidence)

I'm still mystified.