I stumbled on this while trying to finally understand the Butterworth filter in the Pd audio examples (see "H13.butterworth.pd"). Studying the calculation of the filter coefficients I was wondering how the locations of the real pole and zero were different from those of the 1st order filter. So I compared it with a one-pole, one-zero lowpass filter, ELSE's [lop2~].
Well, yes, there are differences ... But here's the strange thing: My filter with the coefficients calculated exactly like in the Butterworth filter behaves as I would have expected, whereas ELSE's [lop2~] doesn't work too well in the high frequency range. This is even stated in the help file.
Here's how I tested the filter: lop2-test.pd
Can anyone explain this? Am I missing something?

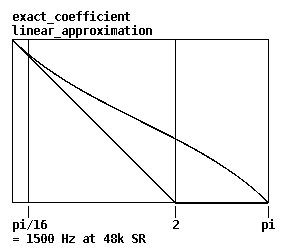

 I suspect that a number of ELSE signal objects are cribbed from SC, or cribbed from the same source of DSP formulas that SC cribs from (e.g, [resonant~] vs SC's
I suspect that a number of ELSE signal objects are cribbed from SC, or cribbed from the same source of DSP formulas that SC cribs from (e.g, [resonant~] vs SC's