This may be complete BS, but here goes: when I convolve a 1s piano chord sample with 30s of stereo white noise, I get 30s of something that almost sounds like it's bubbling, like the pianist is wiggling their fingers and restriking random notes in the chord (what's the musical term for that? tremolo?). It's not a smooth smear like a reverb freeze might be. I assume that's because the constituent frequencies of the noise have varying volume over time. If I'm right, I think I should be able to increase the bubbling effect by increasing the volume variation of each frequency and/or making the rate of volume variation change more slowly. For lack of a better understanding of noise I'm calling this "coarse-grained noise." Is that a thing? Am I on the right track? How would you generate such noise? I'm thinking of using an [irfft] and making each coefficient vary more widely but more slowly, but I would not be surprised if that's way off the mark.

Just a little warning: In subpatches with overlapping windows [noise~] doesn't output new values for each window but only for each block. (At least I hear artifacts that led me to this conclusion.) It seems like it can be fixed with [bang~] --> [random] --> [seed( --> [noise~]

@manuels I was not prev aware of these other kinds of white noise but they are all smooth and so don't produce the kind of texture I want. To give you a sense of what I'm looking for, here is the sound of a drip into an empty tin can: tinCanDrip1.wav. Convolved with binary white noise, you get this: tin can conv binary noise.wav. Now here is my nasty-sounding whitening of bubbling water and it's convolution with the tin can: whitened bubbling.wav & tin can conv whitened bubbling.wav. See how the result sounds a little like a small stone being rolled around the bottom of the can?

Also, that's interesting about [noise~] in overlapped windows, I'll go back and modify my version of that patch to see if the lo-fi mp3 quality goes away.

@whale-av "randomly modulated in its amplitude"--yes, that's what I tried with the 64 band 1/5 oct graphic. It's not bad, but it's not natural sounding either. Could be useful anyway, depending on the effect you want.

@ddw_music My problem isn't the convolution (I'm using REAPER's ReaVerb for that), I'm just wondering how to make the kind of IR that produces the effect I want. Your rifft strategy is what I speculated about in my original post and what I first tried using [array random] to generate freq domain moduli with a similar distribution as [noise~]. FYI Pd's real inverse FFT automatically fills in the complex conjugates for the bins above Nyquist, so you don't have to write them--leaving them as all 0 is fine. Also note that your [lop~] is filtering the change between successive bin moduli in a single window, not the change of each bin from window to window. I'm speculating that the latter (maybe using asymmetric slewing rather than low pass filtering) would make frequency peaks hang around longer (and hence more audible) whereas I'm not sure what the former does. That said I think the strategy of modifying natural sound is paying off faster than these more technical methods.

@jameslo Thanks for the audio examples! Sounds a bit like dense granular synthesis to me.

If you want to follow the FFT / lowpass filtering approach: You could simply rebuild the filter so that it operates between successive FFT frames like this: ugly-noise.pd
The "sample rate" of this lowpass filter is then of course SR/hopsize, which is why the lop frequency can only reach up to about 120 Hz.

I'm still wondering if you can't get similar results with time domain manipulation of white noise, for example if you chose a rather extreme shaping function like say exp(-1000*x^2).

@jameslo said:

FYI Pd's real inverse FFT automatically fills in the complex conjugates for the bins above Nyquist, so you don't have to write them--leaving them as all 0 is fine.

Ah. OK -- I hadn't guessed this, as there seems to be no statement to that effect in the help file.

Also note that your [lop~] is filtering the change between successive bin moduli in a single window, not the change of each bin from window to window.

A legitimate blunder -- quite right. In any case, it was kinda cool to see that simulating the behavior of Fourier partials for white noise did seem to produce clean white noise.

hjh

@manuels I was expecting to have to sit down with pad and pencil to figure out how to do the low pass filtering sideways, but there you've done it in ugly-noise.pd. Thanks!

BTW I added your noise reseeding trick to my version of that rifft~ noise generator and one repetitive artifact went away but the general crappy mp3 vibe stayed the same. It seems to be correlated with wider moduli distributions.

I would happily try waveshaping noise if I understood better what kinds of results to expect. Maybe you could elaborate further? I tried the extreme function you suggested but I feel like there must be parens missing in the expression and I don't know what would constitute good parens.

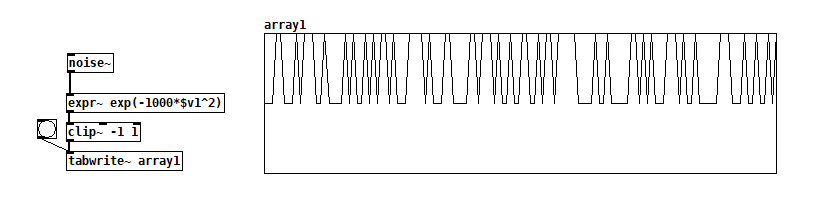
@jameslo Oh, [expr~] obviously can't handle this kind of pow notation ... So what I suggested (pretty arbitrarily, to be honest) was just a skinny Gaussian curve. Try exp(-1000*$v1*$v1) instead.

The intuition behind my choice was quite simple: First off, I thought it might be useful to reduce the density of the echoes of the input sample. In fact, convolution does produce "echoes" at every sample, although most of them won't be heard as echoes but as filtering effects. Furthermore, the exponential function has the useful property to be bounded between 0 and 1 for negative input values, and it seemed to be a natural choice, since it corresponds to our perception of amplitude.

Trying to generalize on how to use a transfer/shaping function in this specific case: The input (noise) is equally distributed, so the distribution of the output will be exactly the same as the distribution of the shaping function itself. If I correctly understand the concept of white noise, any shaping function will also produce white noise as its output. The "color" of noise is only affected, if the operation introduces some kind of correlation between successive samples. That's what all digital filters do, of course. So now you may ask: Then why does waveshaping in its conventional use affect the timbre of a sound? Well, usually successive samples of an input signal aren't uncorrelated, right? A transfer/shaping function then will have some impact on the existing autocorrelation of the sound. So the case of applying such a function to white noise is really quite specific.

BTW: Thinking about distributions of sample values also helps to understand the RMS amplitude of differently distributed white noise signals: Equally distributed noise has the same power as triangle and sawtooth waves, whereas binary noise has the greatest possible power, equal to square waves etc.

Hopefully, this does help in some way ... Apart from that, I would recommend to implement the transfer function as a lookup table and draw different curves. I think, this might be the best way to get an intuition of how a waveshaping transfer function works.

Edit: Drawing the histogram instead of the transfer function may be even more intuitive, especially if you already know how to use [array random]. So here's basically an audio rate version of that ... array_random~.pd

@manuels So judging from your patch, it's not essential to have all waveshaped noise output samples be either 0 or positive?

BTW I tried the corrected version of the skinny Gaussian curve and the resulting convolution sounds rough textured, but not as coarse as the whitened bubbling. Still might be useful though.

@jameslo said:

@manuels So judging from your patch, it's not essential to have all waveshaped noise output samples be either 0 or positive?

It's certainly not essential, maybe not even preferable, but I'm not sure about that. Wouldn't a purely positive valued signal produce DC if there was some in the signal it's getting convolved with?

@manuels I'm just trying to infer the kinds of waveshaped noise that you think might have potential based on what you gave me. The skinny Gaussian curve produces zeroes in most places and positive spikes everywhere else. But your patch can produce positive and negative output samples as well as signals that have DC offset. Plus it's much harder to output long runs of zeroes.