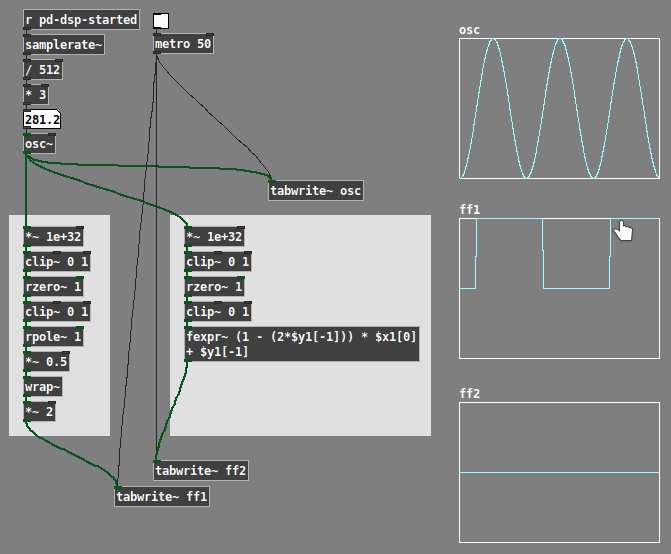
I was just pondering a signal-rate flip-flop toggle.
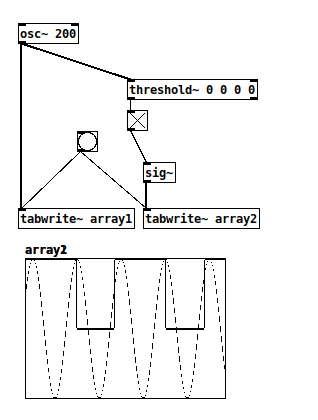
The "easy way" is a pulse counter, modulo 2 (left side). This works, but will eventually overflow.
Then I thought... if you have a "true" signal a, and a "false" signal b, and a condition signal x (0 or 1), then if(x, a, b) == (a-b) * x + b (algebraic reduction of a*x + (b * (1-x)) = ax + b - bx).
If the "true" signal flips the last output -- a = 1 - y1[-1] -- and the false signal just outputs the previous value -- b = y1[-1] -- then:
((1 - $y1[-1]) - $y1[-1]) * $x1[0] + $y1[-1]
(1 - (2 * $y1[-1])) * $x1[0] + $y1[-1]
... which does satisfy the cases:
- if $x1[0] == 0, the first term disappears and it outputs the previous sample, ok.
- if $x1[0] == 1:
- if $y1[-1] == 0 (as it is initially), then: (1 - (2*0)) * 1 + 0 == 1, ok.
- if $y1[-1] == 1, then: (1 - (2*1)) * 1 + 1 == -1 + 1 == 0, ok.
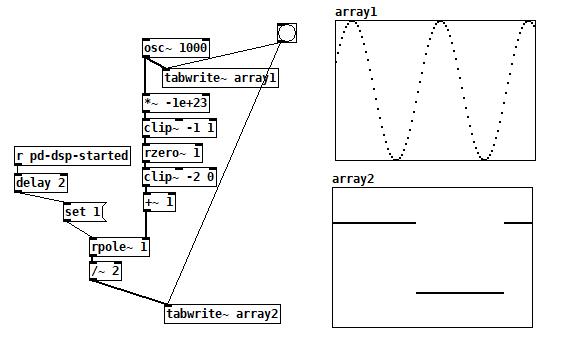
So, in theory, that should work in fexpr~. But I only get zeros.
I can imagine only a couple of possibilities. One is that I misunderstood what is $y1[-1]. The other is that there might be a bug.
(Yes, I know fexpr~ is slow... but it should be able to do this, no...?)
Just before posting, I tried replacing $x1[0] with $x1[-1] and... it starts toggling! Uh... why? In theory I should be taking the current trigger sample vs the previous output sample, which is what I wrote, but it only works to take the previous trigger sample...? (Point being, if I did this in a class, I couldn't explain why $x1[0] is bad while $x1[-1] is good. These are all deterministic operations, so it should be explainable.)
EDIT: Checking the tables' list views, I found that the fexpr~ with $x1[-1] is one sample late... confirming that $x1[0] is theoretically correct. So I'm puzzled why it fails.
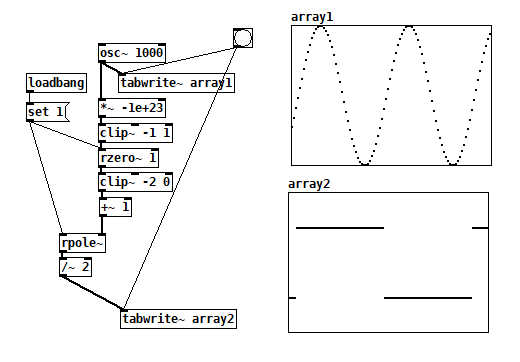
EDIT EDIT: After quitting and relaunching Pd, $x1[0] works  soo... never mind... weird.
soo... never mind... weird.
hjh